主題名稱:校園中無所不在的黃金面紗
作品學習領域:數學
施行年級:4年級
學生人數:26人
課程節數:2節
媒體影音來源:
比的應用 I
比的應用 II
█ 教學發想(教學活動概述)
當我就讀國小、國中時,老師所教授的數列通常是在尋找有規律的數列,例如:
(1) 2、4、____、8、10、 14、 ___
(2) 1、4、____ 、16、____ 、36……等等,自已當上老師之後曾試圖想過,與其要學生找數列有什麼規律性,倒不如讓學生了解數列及數字有什麼特質及意義,而費波納契數列在國小及國中學習階段很少被提起過,只有在談論到黃金比例的現象時會涉入到費波納契數列,甚至大多數的學生還不清楚黃金比例是由費波納契數列創造出來的,故本次課程方案顛覆傳統數列的教學法,以創新教學法讓學生理解黃金比例的值Φ=0.618 是由費波納契數列推導而來的。
█ 教學流程(過程)
教學流程
步驟一:讓學生認識費波納契數列,並請學生先思考費波納契數列和黃金比例的關聯性為何?接下來引導學生由費波納契數列推導黃金比例的值。
步驟二:在國中課程當中,有許多單元和費波納契數列有其關聯性,教師先安排問題的情境(提示和那個單元有關)→提供思考與醞釀的機會(請同學思考課程單元和費波納契數列關聯性)→尋求解決問題的方法來進行(同學先獨立思考之後,並和同組學生討論其關聯性為何?),以培養學生獨立思考及團體合作之能力。
步驟三:帶領學生實際觀察生活及校園中存在費波納契數列與黃金比例的現象,在生活當中,Apple logo、雛菊…等等符合黃金比例現象;在校園中,多種植物的朵數符合費波納契數列,而蒙娜麗莎的微笑這幅畫也符合黃金比例的現象,最後並請同學思考生活周遭中,還有那些案例和費波納契數列及黃金比例有關聯性。
█ 教學過程
一、一切都從兔子的故事開始
由「三生一死的費氏數列」教學文獻當中,先讓學生思考以下問題:
老師問:如果一對兔子從第二個月開始,每個月會繁殖一對兔子,那麼將一對兔子放在一塊圍起來的區域內,一年後共可繁衍多少對兔子(假設兔子都長生不死的話)?
教師藉由兔子的故事讓學生發現費波納契數列的規律,並推導出其計算公式。
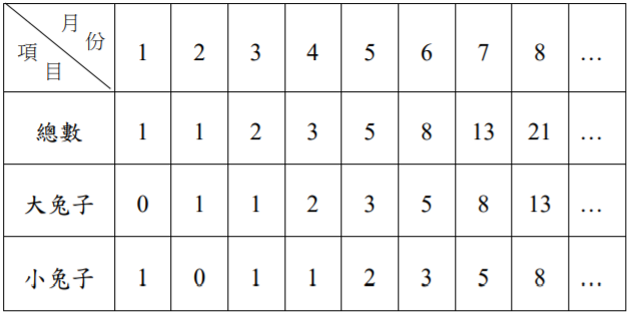
學生答:老師,我們從免子月份的總數可以發現其數列為1、1、2、3、5、8、13、21、34、55、89、144…,任意取三個連續的數,其前兩項和就是第三項。
老師總結:若以代表第n 個費波納奇數列,費波納奇數列公式如下:
![]()
老師問:請問同學有沒有聽過什麼叫黃金比例。
學生答:老師!我聽過清玉飲料店的黃金比例,還有人體身材的黃金比例!
老師說:同學回答非常的棒,黃金比例除了在國中一元二次方程式單元中的黃金矩形有被提起過之外,其實它與費波納契數列也存在密不可分的關係,接下來老師將帶領同學由費波納契數列推導黃金比例的值。
老師說:請同學將費波納契數列的前後相鄰兩項相除,可以得出什麼結果(同學可以使用電子計算機)。
同學答:愈後面的費波納契數列任相鄰兩項相除,其結果為趨近0.618 或1.618。
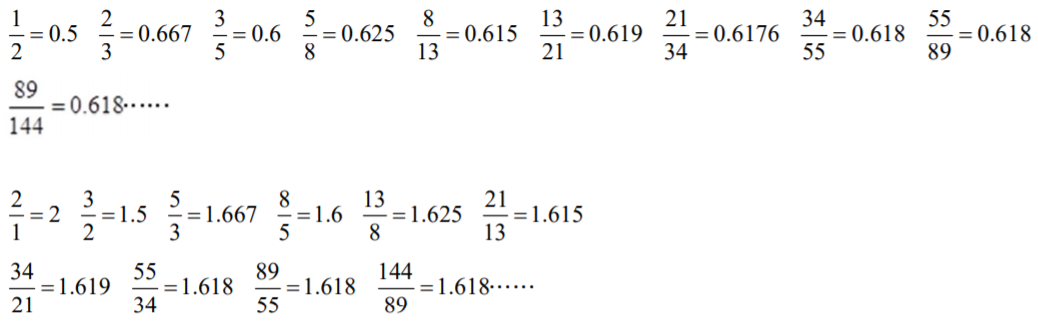
二、生活中的黃金數
老師說:同學已經知道黃金比例是由費波納契數列推導而來,各位同學知道嗎?其實費波納契數列與黃金比例就存在你我的身邊!
同學答:真的嗎?在那邊?
老師說:像老師的蘋果手機logo 就是符合黃金比例的現象,老師現在將Apple logo 印在A4 紙上請同學測量其長度,請同學按以下步驟進行。
STEP 1 請學生先用直尺測量下圖Apple logo 中,A 線段、B 線段(B=D)、C 線段及E 線段的長度。
STEP 2 請學生算出以下的比值 A/B、C/D、E/D。
STEP 3 請各組分享算出來的值為多少?,是否趨近於黃金比例。
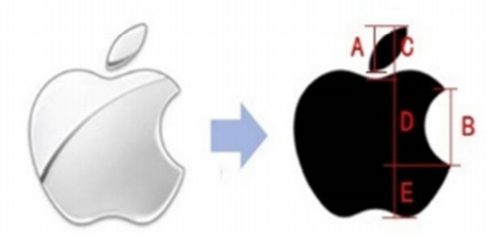
同學答:測量結果為 D=6,A=3.3,C=3.7,B=5.2,E=3.5。
老師說:我們將A 除以B 得0.615,C 除以D 得0.616,兩數值皆趨近於黃金比例的值0.618,可見已故蘋果創辦人賈伯斯已有黃金比例構圖之的思巧。
老師說:除了Apple logo 符合黃金比例的值之外,像是植物中的雛菊也有此現象,下圖為雛菊雙螺旋結構的分解圖,請同學計算雛菊順時針方向和逆時針方向有幾條?
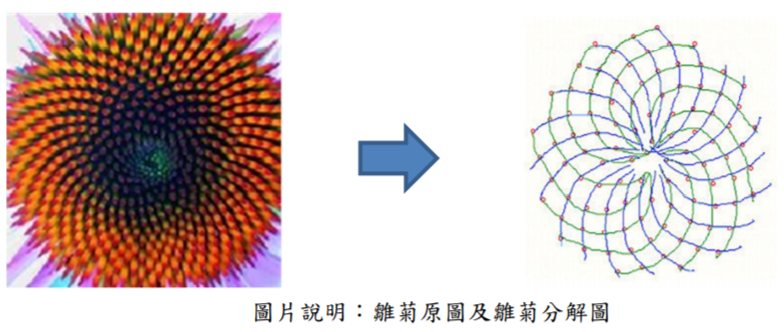
學生說:順時針方向有21 條,逆時針方向有13 條,13 和21 剛好是費波納奇數列中兩個相鄰的數字。
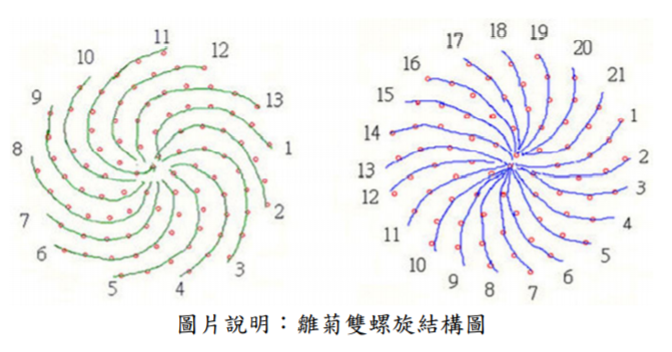
老師說:13 和21 這兩個數字為費波納契數列,我們將13 和21 相除可以得到值為0.618,故雛菊也是黃金比例的概念。
三、校園中的奧秘
老師說:校園中存在許多符合費波納契數列及黃金比例的現象,老師接下來將帶領大家在校園中進行觀察喔!

學生說:老師,我們發現校園的植物當中,有許多符合費波納契數列為5 的花朵片數,例如:沙漠玫瑰5 片、軟枝黃蟬5 片、咸豐草5 片,想不到費波納契數列這麼神奇。
老師說:校園當中還有許多植物也是符合費波納契數列,就連法國巴黎羅浮宮的「蒙娜麗莎的微笑」也是黃金比例值的概念,夠神奇吧!!
四、參考文獻
1.影片名稱:比的應用I,製作者:國立教育資料館,出處:教育雲教學媒體影音。
2.影片名稱:比的應用II,製作者:國立教育資料館,出處:教育雲教學媒體影音。
3.主題:三生一死的費氏數列,作者:林映辰、呂安培 (新北市三峽區龍埔國民小學),出處:中華民國第53屆中小學科學展覽會作品。
4.主題:費氏數列,作者:許家蓁,出處:教育大市集。
█ 教學現場發現
本次教學活動以十二年國民教育課程綱要數學領域核心素養為主軸,結合跨領域教學及計算工具的使用,讓學生擁有「自主行動」、「溝通互動」及「社會參與」之三大核心素養面向之能力。本次教學現場發現如下:
一、在費波納契數列推導黃金比例值時,將費波納契數列相鄰兩項相除時,因會有小數點數值的發生,故讓學生利用電子計算機計算時,可以避免較繁瑣的數值產生,提高學生願意計算之意願,並熟練計算工具之使用。
二、在費波納契數列與國中課程關聯性當中,老師可以先安排問題的情境→提供思考與醞釀的機會→尋求解決問題的方法來進行。老師先提示費波納契數列與某單元主題有關,請學生用費波納契數列之性質來驗證與某單元之關聯性,再請學生們思索問題並回饋,讓學生們有腦力激盪的機會。
三、在本教學活動中,有許多案例是符合費波納契數列與黃金比例的現象,老師可以再請學生去尋找生活及校園當中,還有是屬於費波納契數列與黃金比例的個案,並與同學們分享,培養學生發現問題與解決問題之能力。
四、本次教學屬於創新教學的課程,創新課程固然可以帶動學生的學習興趣,提高學生的學習動機,但有可能是學生第一次接觸費波納契這個數列,學生們難免會有生疏感的情況發生,故下次再上創新課程時,宜事先與同學們溝通及討論,如同學於上課有較聽不懂的細節,於課後進行補救教學,讓同學們不會擔心聽不懂、學不會,讓孩子們快樂學習。
█ 教學反思與收穫
以創新教學方式提高學生學習動機,帶領學生改變學習數字規律性的思維,以費波納契數列的概念引導黃金比例的值及和國中數學的關聯性,並讓學生實地觀察校園中存在費波納契數列的現象,讓學生驚呼連連!體會費波納契數列的奧妙之處,同學們紛紛表示希望能多多上此類型的創新課程,我並期許之後能以「翻轉教育」的教育方式,展現不同的上課方法,讓同學們有動力的學習,培養學生創造思考能力,讓我們與學生們一起「翻轉」吧!
█ 教學照片

